ABSTRACT

Attempts to describe aesthetic artefacts through informational models have existed at least since the late 1950s; but they have not been as successful as their proponents expected nor are they popular among art scholars because of their (mostly) quantitative nature. However, given how information technology has deeply shifted every aspect of our world, it is fair to ask whether aesthetic value continues to be immune to informational interpretations. This paper discusses the ideas of the late Russian biophysicist, Mikhail Volkenstein concerning art and aesthetic value. It contrasts them with Max Bense’s ‘information aesthetics’, and with contemporary philosophical understandings of information. Overall, this paper shows that an informational but not necessarily quantitative approach serves not only as an effective means to describe our interaction with artworks, but also contributes to explain why purely quantitative models struggle to formalise aesthetic value. Finally, it makes the case that adopting an informational outlook helps overcome the ‘analogue vs digital’ dichotomy by arguing the distinction is epistemological rather than ontological, and therefore the two notions need not be incompatible.

KEYWORDS

Aesthetics; Artwork; Complexity; Information; Pattern; System.

1. INTRODUCTION

Recent developments in Information and Communication Technologies (ICT) have led to profound socio-cultural changes and paradigm shifts. The ‘information cycle’ (Floridi, 2010) has become the engine of post-industrial societies and information itself has turned into a powerful hermeneutical device employed by many scientific fields to comprehend and explain a myriad of phenomena. Even the humanities, a field historically wary of ‘technoscience’, have come to embrace ICTs and informational approaches through so-called ‘digital humanities’ institutes and programs. Creative practitioners now regularly use computational tools and methods and, in the process, are expanding the limits and transforming the ‘languages’ of aesthetic practices, as well as our wider understanding of art and humantechnology relations. Nonetheless, and although computational technology is quintessentially informational, information-centric analyses of art continue to be rare. Arguably, this has to do with the fact that information is still regarded by scholars in the arts and the humanities as a purely quantitative notion. Hence, it is associated with formalisation, and systematisation; modes of thinking that are seen as threats to art’s strongest features: its intuitive nature and its openness to interpretation.

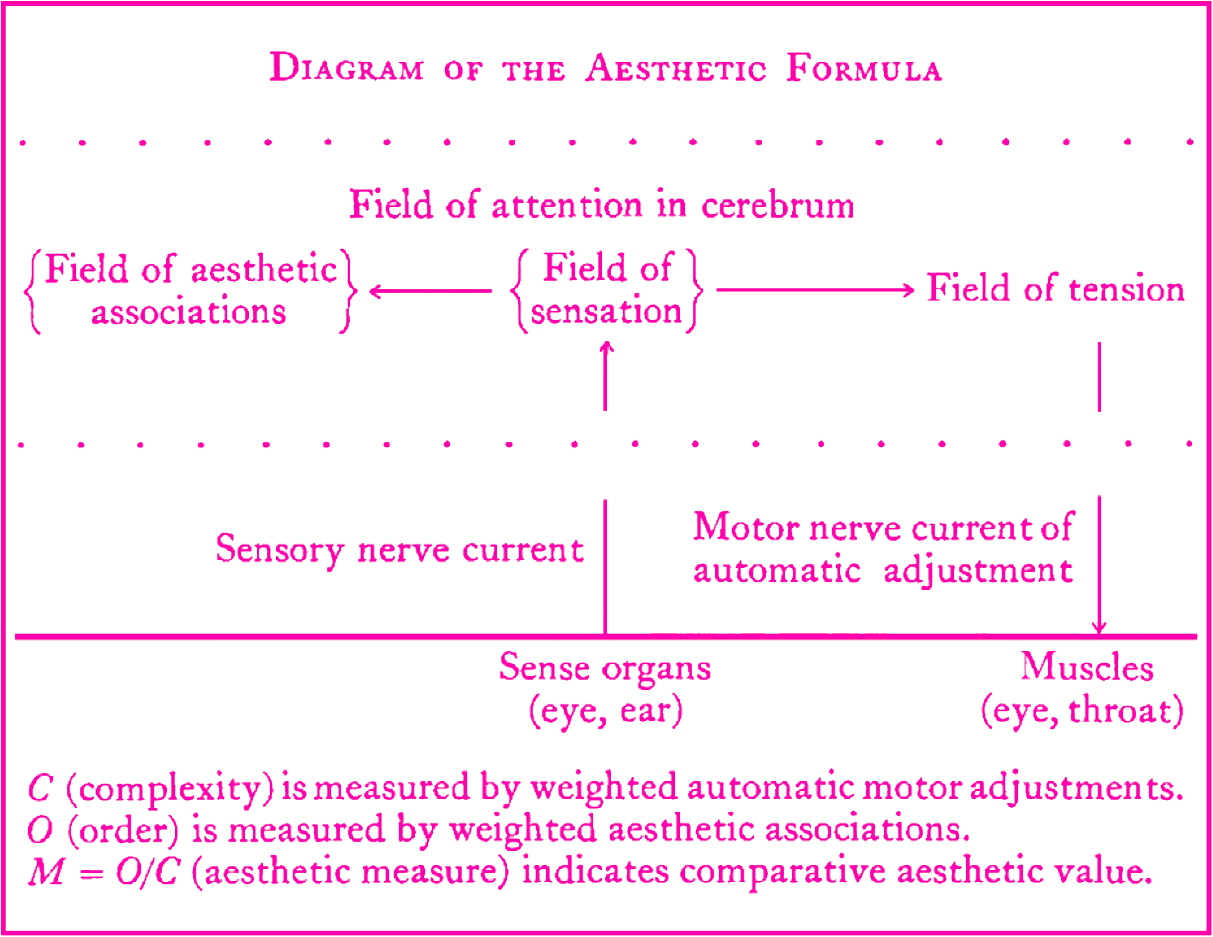
COMPENDIUM Note: The diagram presents analysis of the aesthetic experience and the basic Birkhoff's aesthetic formula. Source: Birkhoff, G.D., 1933. Aesthetic Measure. Harvard university press, Cambridge, Massachusettes.

The most well-known attempt to analyse aesthetic value through an informational lens was Max Bense and Abraham Moles’s ’informational aesthetics’. Developed in the late 1950s, this was a multidisciplinary approach that mixed George D. Birkhoff’s (1933) ‘aesthetic measure’, based on the ratio between order and complexity, Claude E. Shannon’s (1948) Mathematical Theory of Communication, Norbert Wiener’s (1985) Cybernetics and Peircean semiotics (see Klütsch, 2012). The ultimate goal of information aesthetics was to develop a method for objectively measuring aesthetic value, thus freeing aesthetic judgements from ‘subjective speculation’ (Klütsch, 2012, p. 67). Understandably, and despite Modernism’s penchant for rationality (e.g. Clement Greenberg’s (1999) comparison between medium specificity and the scientific parcelling of natural phenomena), this type of engagement with artworks was not the most popular within art scholarship, even after computational technology became fully embraced by artists and other creative practitioners. Instead, most contemporary art scholars continue to outsource their theoretical frameworks and views on computer-generated aesthetic artefacts to media studies and other recent fields such as software studies.

This paper discusses Mikhail Volkenstein’s (2009) characterisation of artworks as ‘integral informational systems’. It argues that this informational approach offers not only a rich insight to better understand how we relate and judge aesthetic artefacts, but also helps to clarify why attempts to quantify aesthetic value are very unlikely to succeed. The paper begins by introducing key aspects of information as understood by Shannon’s Mathematical Theory of Communication, as well as providing a brief description of information aesthetics’ main arguments. This is followed by a concise outline of Volkenstein’s ideas concerning artistic information and its value. The next section then introduces an alternative understanding of information, provided by the philosophy of information. The discussion begins by comparing Volkenstein’s views with information aesthetics, before showing why seeing the artwork as a system explains the failure of quantitative models to fully account for aesthetic value. Finally, the paper suggests that by being applicable to all forms of art, the informational system approach discussed above may help supersede the analogue vs digital dichotomy. This paper does not (cannot) deny that aesthetics, creativity and artistic pleasure might someday be analysed objectively; that is, it does not subscribe to any essentialist conception of art. It simply shows that trying to quantify what happens when we create art amounts to quantifying human cognitive abilities; a task which, at the very least, would, call for enormous datasets, computational power, and algorithmic design way beyond our current capabilities.

2. UNDERSTANDING INFORMATION

The word information from the Latin term in formare, is a construction reportedly used by Cicero and Saint Augustine when discussing Plato’s Theory of Forms, and particularly by Cicero to refer to ‘“representation[s] implanted in the mind”’ (cited in Adriaans & Van Benthem, 2008, p. 8). By the early Renaissance, the French word information came to be used interchangeably to refer to such things as ‘”investigation,” “education,” “the act of informing or communicating knowledge,” and “intelligence”’ (Adriaans & Van Benthem, 2008, p. 8). However, by the end of the seventeenth century, the original technical sense of the word had disappeared, as British Empiricists who returned to Platonic sources chose instead to use the term ‘idea’ (Adriaans & Van Benthem, 2008), from ‘eidos’, the Greek word for Platonic Form (Dusek, 2006). It was only in the twentieth century that ‘information’ began to recover its technical connotation. Harry Nyquist and Ralph Hartley, both engineers working separately at Bell Laboratories, became interested in the possibility of quantifying the transmission of information or ‘intelligence’ (Byfield, 2008). Their papers, published in 1928, would serve as the basis for Shannon’s 1948 landmark work, ‘A Mathematical Theory of Communication’ ¹ (henceforth MTC), the first successful method for describing communication in terms of probability, and the stepping-stone for contemporary ‘information theory’ ².

2.1 INFORMATION AS QUANTITY

Although usually described as such, MTC is not a theory of information. It is rather a statistical formalisation of data transmission. And while the theory does provide a definition of information (i.e. as a measure of the freedom of choice an agent has when selecting the contents of a message), it is so intentionally narrow as to be hardly useful outside the theoretical framework in which it is embedded. Oversimplifying, Shannon’s theory is a general description of the circumstances governing every instance where ‘not-yet-meaningful’ data are transmitted (Floridi, 2016), and which are represented by computable and interchangeable binary digits, or ‘bits’. The goal of MTC was not to provide an allencompassing account of information, but to determine (a) what the ultimate level of data compression was and (b) what the ultimate rate of data transmission was. In other words, how much could the size of a given message be reduced before making it unintelligible and how fast could it be transmitted. For MTC, ‘information’ does not refer to what is actually being said, but instead to what could be said (Weaver, 1949) using a given amount of data.

Since MTC was conceived to analyse any instance of information exchange in quantitative terms, the model had to ignore all the unquantifiable ‘psychological’ (Byfield, 2008) aspects involved in communication. MTC intentionally disregards the semantic value of messages and treats information as a mere placeholder – in the same manner that a gram and a millimetre serve as placeholders – that is, as a ‘raw’ (Floridi, 2004, p. 51), ‘dimension-less’ (Ben-Naim, 2008, p. 203) quantity. MTC is fundamentally a model of communication limits at the syntactic level, concerned exclusively with the transmission of information and not with information itself. This means MTC has little to say about reception (an aspect of communication which is of capital importance to, say, media theory). Moreover, MTC does not provide a method for measuring information per se but for quantifying the amount of ignorance or uncertainty erased by a message (Floridi, 2004). In other words, Shannon used the quantification of predictability and redundancy as a ‘backward way of measuring information content’ (Gleick, 2011b, p. 191).

MTC regards communication as a system that is neither deterministic nor entirely random, but stochastic, meaning that its outputs are the product of certain probabilities (Gleick, 2011a, p. 187). Two fair dice are an example of a stochastic system since it is possible to calculate the probability of getting any number between two and twelve at any given throw; with seven being always the most probable outcome, and with each throw being subject to a certain amount of randomness, or ‘entropy’, and probability. Conversely two extremely biased dice represent a deterministic system, since after a series of throws one can be fairly certain of what number will come next. Deterministic systems are virtually devoid of randomness. Whereas in a totally random system (i.e. one that stands in a maximum state of entropy) the succession of events shows no discernible pattern on which to base future predictions, for there is simply no way to calculate the likelihood of any output. For MTC, the more unexpected the contents of a message the more informative the message is and vice versa, the more expected and redundant the less informative. Thus, in theory, the higher the randomness, the higher the (potential) amount of information. In summary, for MTC information represents a decrease in uncertainty or, more precisely, a reduction in ‘data deficit’ (Floridi, 2004, p. 47) or ‘ignorance’ (Ben-Naim, 2008) about the state of a system or the contents of a message. MTC is a very effective model in contexts where semantic value is not a priority – e.g. in electronic communications and computation, but its suitability diminishes greatly in circumstances where meaning is central to the analysis, such as in aesthetic practices.

2.2 INFORMATION AESTHETICS

One of the most well-known attempts to apply MTC’s definition of information to the analysis of aesthetic artefacts was ‘Information Aesthetics’. This theory’s goal was to measure the amount and the quality of information present in aesthetic objects and hence facilitate their objective and scientific judgment (Klütsch, 2012, p. 67). Information aesthetics was originally developed by Max Bense and Abraham Moles between 1956 and 1958. These two researchers were very influential figures in the socalled ‘Stuttgart School’, a group around which many digital art pioneers gravitated. Information aesthetics reinterpreted concepts such as ‘process’ and ‘entropy’ as seen by physics and MTC under Peirce’s pragmatic semiotics, and merged them with Birkhoff’s ‘aesthetic measure’ (1933) conceived as a ratio between order and complexity – hence, the lower the complexity, the higher the order and the aesthetic value. Bense, regarded artworks as signs that could be broken down into isolated elements (primitives) that could then be treated as the building blocks of algorithmic processes (Klütsch, 2012). He imagined art as a process of aesthetic production, consumption, and criticism whose workings could be formalised in terms of an axiomatic system.

COMPENDIUM Note: George D. Birkhoff's theory of aesthetic measure and its applications to geometric forms to provide systematic means of analysis in simple formal aesthetic domains. Source: Birkhoff, G.D., 1933. Aesthetic Measure. Harvard University Press, Cambridge, Massachusettes.

The key assumption information aesthetics made – or at least that Bense made – was that creative processes generally produce order (Rigau, Feixas & Sbert, 2008) or ‘negative entropy’ out of disorder. This idea is closely connected to Boltzmann’s identification of entropy with disorder (Ben-Naim, 2007, p. 196). According to this interpretation, physical processes tend to change from initial more ordered states, towards a state of maximum entropy or ‘“mixupness”’ – as described by the polymath J. W. Gibbs (Ben-Naim, 2007, p. 198), a key figure in the development of statistical mechanics. Thus, as Bense saw it, while the physical world is inevitably poised towards chaos (i.e. to a state of maximum entropy), aesthetic creation strives towards order or ‘negentropy’ (see Klütsch, 2012). It is in the relation between chaos/complexity and order that aesthetic value lies; and for Bense this framework has the status of a natural law. The aesthetic object has special properties that go beyond its material carriage; a ‘correality’ that is determined by ‘macroaesthetic rules’ which may be interpreted and modelled through objective algorithmic processes. By surrendering subjective interpretation, Bense and Moles’s not only gave up on aesthetics as ‘a theory of sensual perception’ (Nake, 2012) but also on the notion that ‘the subject matter of aesthetics is in itself intrinsically subjective’ (Cohen et al., 2012).

3. THE ARTWORK AS AN INTEGRAL INFORMATIONAL SYSTEM

In the last chapter of his (2009) book, Entropy and Information, the late Russian biophysicist Mikhail Volkenstein offers an informational interpretation of aesthetic value. The core premise of his model is that creating art involves generating new and irreplaceable information. In other words, that artistic creation implies ‘the fixing, the committing to memory, of random choices’ (Volkenstein, 2009, p. 186). Artworks thus may be regarded as non-isolated ‘integral informational systems’ that not only comprise but – most importantly – also further generate new information. They are non-isolated because once entering the world, artworks acquire a life of their own, potentially interacting with an audience while maintaining a linkage with their creators. Artworks are integral systems because – as happens with living organisms – all their features are indispensable for proper functioning, and even the slightest change in their internal structure can potentially alter their whole meaning. That is why a single word in a poem can potentially downgrade a masterpiece to tackiness.

3.1 CREATING NEW AESTHETIC INFORMATION

Because every artwork is open for interpretation, every person is entitled to say whether they like it or not. Nonetheless, a competent and serious judgment calls for the observer to have a ‘thesaurus’ (Volkenstein, 2009, p. 188), that is, certain background knowledge, aesthetic sensibility, and willingness to interpret the artistic information being conveyed. That is why the receptor effectively plays the role of co-creator of the piece. Furthermore, reception of artistic information involves both a partial loss as well as an ‘enhancement’ of information, just like every instance of communication is potentially subjected to the interference of noise ³, originated in the physical and environmental conditions surrounding the transmission. Given the unsurmountable gap between the mind of the artist and the minds of her audience, a certain amount of information conveyed by her artwork is bound to dissipate in the process of being received. For Volkenstein (2009, p. 187) such loss is ‘inevitable’ and ‘trivial’. What is not trivial is the fact that the artwork ‘activates or programs [emphasis added] a stream of associations, thoughts, and feelings in the consciousness of the receptor’ (Volkenstein, 2009, p. 188) stimulating the creation of new information by him or her. In summary, according to Volkenstein, the true value of an artwork resides not in the object itself but in what it brings about in the audience engaging with it.

3.2 THE VALUE OF ARTISTIC INFORMATION

For Volkenstein, the value of the information generated by an artwork depends largely but not exclusively on its singularity and irreplaceability. The more novel and unexpected the information a given artwork generates – i.e. the less redundant it is – the more valuable it will be. But regarding this point Volkenstein (2009, p. 188) notes an important caveat: whereas for MTC redundancy is normally equated to low informativeness, in the context of art the equivalency cannot stand, since many artworks use repetition precisely as an aesthetic device. Therefore, a truly redundant and uninformative artwork will be so on the basis of cliché and banality, or because it merely stands out due to technical prowess. Volkenstein thus generalises: the value of a work of art may be seen as directly proportional to the novelty and unexpectedness of the information it conveys. Nevertheless, however indispensable newness might be, it is not a sufficient condition for the emergence of artistic value. This is illustrated by the fact that a given artwork might simply be a derivative and or mediocre exemplar of an already established genre, thus it cannot generate valuable information beyond its own ‘matter of factness’. A true artwork needs to not only convey, but also stimulate the production of new information.

Volkenstein is aware that aesthetic judgements do not happen in a vacuum, but that artworks are interpreted according to fluctuating tastes and socio-cultural norms. Reception of artistic information is both a collective and a personal matter subjected to historical and psychological changes. That is why yesterday’s mediocrity may become today’s masterpiece and vice versa. The timeless masterpiece is thus the artwork to which we ’return’ repeatedly over the course of our lives and that always seems to offer something new; true ‘genius’, as Volkenstein (2009, p. 190) argues, ‘is unlimited informativity’.

Volkenstein describes art as a process that creates order out of a primeval chaos, but also as a peculiar form of knowledge of the world. He sees entropy as directly opposed but also indispensable for the emergence of art; since it is precisely a lack of uniformity which allows the poietic ‘negative entropy’ to emerge and be noticed. Contrary to more fatalistic interpretations of entropy, Volkenstein sees this phenomenon as an imperative condition for life since without it there would be no movement, no transference, and no change.

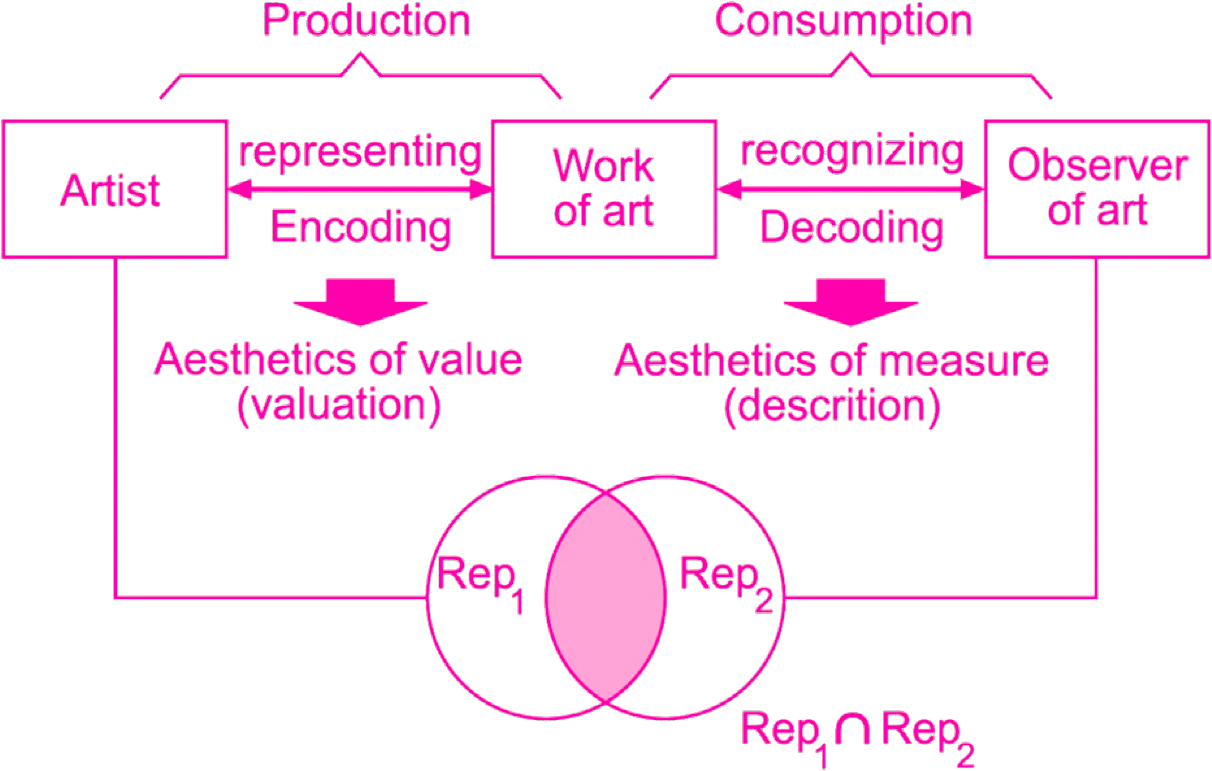
COMPENDIUM Note: Max Bense's System of Aesthetic Communication. Informational Aesthetics-What is the relationship between Art Intelligence and Information. Source: https://www.jadm.eg.net/cgi/viewcontent.cgi?article=1003&context=journal.

4. BEYOND INFORMATION AS A QUANTITY

4.1 INFORMATION AS SEMANTIC CONTENT

The very reason MTC is such an effective tool for information technologies (namely, its disregard for semantic content) makes it comparatively limited within the humanities. Quantitative models neglect granular detail and individual cases because operating at a higher level of abstraction allows them to explain phenomena in more general terms. Science, after all, is about compressing the largest amount of information about any given phenomena into the shortest and simplest explanation ⁴. In the context of art, however, the assumption is that every artwork represents a unique irreplaceable instance, even though it may share some qualities (physical or otherwise) with other exemplars of its class. When we approach works of art, we do it with a hermeneutical intent attuned to granular detail. Hence, the question is what benefits does it have to talk about art in terms of information when the very formulation of this concept seems to ignore its most crucial aspects? – namely, semantic content and its reception. Luckily, as Shannon (1980) himself recognised, MTC’s reductive characterisation of information is by no means the only one available.

4.2 THE GENERAL DEFINITION OF INFORMATION

Most fields related to information science now tend to agree upon an operational definition of information based on semantic content (Floridi, 2011b). According to this ‘General Definition of Information’ (GDI) semantic contents may be considered information if, and only if they are composed of ‘well-formed meaningful data’ ⁵ (see Floridi, 2004; Floridi 2011b). Along with rejecting the possibility of data-less information, GDI requires data to have some form of representation (e.g. binary digits) and also – given the nature of current computational technology – physical implementation ⁶. Now, regarding the question of how or why data can carry meaning in the first place is, according to Floridi (2004), one of the most difficult problems for semantics and human cognition in general. Nonetheless, it is possible to bypass this problem by assuming the issue ‘is not how but whether data constituting information as semantic content can be meaningful independently of an informee’ (Floridi, 2004, p. 45). Examples such as the Rosetta Stone ⁷ and the growth rings in tree trunks show the answer is that meaning is not – at least not exclusively – in the mind of the human subject (Floridi, 2004).

4.3 TWO TYPES OF SEMANTIC INFORMATION

Understood as semantic content, information comes in two major flavours: instructional and factual. Instructional information – also known as ‘imperative’ information – is the kind one might find in stipulations, orders, recipes or algorithms. These instances have a semantic dimension, since they have to be interpretable and therefore meaningful, but unlike instances of factual information, they cannot be correctly qualified in terms of falsehood or truth, only perhaps as being correct or incorrect ⁸. Instructional information does not convey specific facts nor does it model, describe or represent ideas; it merely helps to ‘bring about’ (Floridi, 2016) (factual) information. For its part, factual information (also known as ‘declarative’ information) is the most important of the two kinds of semantic content, but it is also the most common way in which information in the capacity of information ‘can be said’ (Floridi, 2004). Factual information ‘tells the informee [agent] something about something else’ (Floridi, 2004, p. 45); for example, the location of a place, the time of the day, an idea, a fact, etc. To borrow a metaphor from Floridi (2004), factual information is like the ‘capital’ or centre of the ‘informational archipelagos’, since it provides both a clear commonsensical grasp of what information is, while linking all other concepts related to information.

5. DISCUSSION

5.1 TWO INFORMATIONAL MODELS

Volkenstein, like Birkhoff, saw order and complexity as oppositional terms, but drew a diametrically distinct interpretation out of their relationship. For Birkhoff, orderliness meant intelligibility, which translated into a better grasp of the intrinsic aesthetic structure and value of the artwork by the audience. By the same token, complexity obscured order and diminished intelligibility. For his part, Volkenstein understood complexity as a matter of encoding. Following Kolmogorov, Chaitin, and Martin-Löf, Volkenstein saw complexity as the size of the smallest program needed to describe every one of the features of a given object (Volkenstein, 2009, p. 182). The more complex the object, the more complex the description it requires, and therefore the higher the amount of information present in it. Conversely, the more structured or ordered – and hence knowable and expected – an object is, the lower its complexity and informational size. It follows that under this definition – and in accordance with MTC – maximum complexity is equivalent to maximum randomness. However, Volkenstein notes two important caveats: (a) from a descriptive or taxonomic standpoint, complexity is not a fixed quality, but something relative to one’s level of observation; and (b) due to Gödel’s incompleteness theorem, there is no logical way to prove mathematically that a given program/description of an object is in fact the minimal one.

To illustrate the relativity of complexity, we can – as Volkenstein (2009, p. 82) suggests – think of the way a biologist and a butcher regard a bull’s brain: while the former sees a complex system whose minimal detailed specification might require a few millions of bits, the latter sees but one of the couple dozen edible parts of the animal. Similarly, while the word ‘cat’ would take up some twenty-four bits, a picture of a cat might need a few thousand bits, and a (high definition) video of the same cat up to a few million bytes. It follows that, for the time being, encoding the complete specification of that particular cat – or any other organism – in a program shorter than the actual specimen (Volkenstein, 2009, p. 183) is unlikely, to say the least; otherwise, we would be living inside a Borgesian fantasy. Hence, it is safe to say that at least in the former sense every organism in our known world is irreplaceable.

This conception of irreplaceability also applies to artificial objects and, in particular, to works of art. Though it is possible to manipulate and even duplicate certain kinds of artworks, as Volkenstein (2009, p. 183) argues, it is impossible to devise a minimal program for something like Anna Karenina without affecting its overall integrity. Abridging an artwork is by definition a reduction of its informational content and, according to Volkenstein, of its aesthetic integrity and value. Complexity is a matter of structure while irreplaceability, seen in terms of informational value, has to do with added functionality (see Volkenstein, 2009, p. 184). To our photographically sensible eyes, a hyperrealistic painting may be structurally almost as complex in terms of informational size as the ‘real-life’ scene it has encoded, but in truth it contains little new information beyond the factuality of its own existence. For Volkenstein, this type of mimetic art does not say something new and unexpected about something else (its referent), but merely displays the technical skill of its maker. Under Volkenstein’s framework, it is the fact that we learn and do something else with whatever we grasp from an artwork – i.e. that we ‘create new information’ – that truly determines its artistic value. It is not orderliness and recognised formal patterns that are aesthetically pleasing, but the delight of acquiring new, unexpected, and useful knowledge about something in the world.

Volkenstein describes artworks structurally as complex integral informational systems, but functionally as programs that, upon being read, trigger the generation of information that did not previously exist within them. This metaphor allows us to imagine our relation with art in a more contemporary manner. We may describe the artwork as a ‘bootstrap loader’ that launches our ‘thesaurus’, thereby allowing us to generate ideas and connections that we could not have conceived otherwise. We may also think of an artwork not as a pre-compiled program, but more like a complex ‘script’ that may be run through a myriad of interpreters and produce an equally different number of outputs. These could include value judgements ranging from a total lack of interest to considering the artwork a true masterpiece. Nonetheless, like all metaphors, this one also has limits. Unlike computers, our interpreting abilities are not limited to performing numerical calculations and remembering their results; we humans establish complex semantic associations without even trying. As interpreters, we not always consciously ‘choose’ which information present in the artwork we pay attention to and which we ignore. Our interpretations are shaped by our mental and emotional states, by our intellectual and personal backgrounds, and by the very historical and cultural circumstances surrounding our engagement with these and other objects and agents in the world.

5.2 COMPLEX SYSTEMS

Regarding artworks structurally as complex systems clarifies why purely quantitative and supposedly objective measures of aesthetic value are unlikely to succeed, at least for the time being. Complex systems are ‘all about information’ (Taleb, 2012), they arise whenever a given set of autonomous entities – henceforth ’observables’ ⁹ (Floridi, 2011a) – interacting with each other ‘display emergent collective properties’ (see Mignonneau & Sommerer, 2006); and if said properties change over time the system is dynamical (Mainzer, 2004). Because they are filled with intricate interdependencies which most of the time are difficult even to identify, complex systems tend to evolve in non-linear fashions; i.e. they might change in truly unpredictable ways (Taleb, 2012). Since the properties of the system are the result of the mutual interaction of its components, a complex system cannot be analysed by focusing on isolated observables, or even on some of the causal relationships already known to exist between them. Furthermore, the isolated ‘behaviour’ of a system’s element might not even reflect back on the general ensemble. Complex systems call for a somewhat ‘ecological thinking’ (Taleb, 2012) since even the slightest change or disturbance can potentially alter the equilibrium of the entire ensemble. That is why, as Volkenstein argued, complex systems are (necessarily) integral.

Like complexity itself, specified observables are always relative and dependent upon the level of analysis employed to analyse them. Being the source of information about the system, observables are chosen based on the outlook, presumptions, theoretical framework, goals and desired granularity of the observer. Thus, choosing a given observable implies making an ontological commitment – i.e. accepting its existence – which, in turn, is supported by a larger network of beliefs, knowledge, practices, intentions, and instruments (technologies) influencing the experience of the observer. This is why the same system may be analysed and described through different approaches that may or may not share the same observables or even the same definition of a particular observable – and for that matter, of the system as a whole. Hence, observables are not universally ‘objective’, some of them may be subjective or at least far more dependent on the theoretical approach than the observer would like to admit. Such is the case with the notions of complexity and ‘order’ used by Birkhoff and information aesthetics.

Order is a relational as well as a multifactorial phenomenon; it does not (cannot) exist in isolation nor it is a universal value. Patterns, on the contrary, are far more common, pervasive and easier to formalise. As noted earlier, information aesthetics sees art as something that creates order or ‘negative entropy’ and, by the same token, sees entropy, and randomness as equivalent to disorder. Bense’s understanding of the second law of thermodynamics aligns with nineteenth century interpretations of entropy as a force ushering the world towards a state of chaos, uncertainty and dissipation of energy. Along with being pessimistic and subjective, this interpretation is outright misleading. A far more useful way to regard entropy is simply as the tendency of systems to assume their most probable configuration (see Ben-Naim, 2007); whether such state corresponds to ‘disorder’ is a qualitative but not quantitative judgement. This interpretation elucidates why maximum randomness implies maximum informativeness (the absence of a clear-cut pattern allows many other patterns to emerge and for more information to be chosen), and shows why art is not antithetical to entropy. Just as life could not exist without motion (Volkenstein, 2009, p. 169) – without the transference of energy, chemicals, etc. – patterns cannot exist without chaos and randomness. In short, entropy and ‘negative entropy’ (i.e., patterns, structures, art) are opposite but complementary phenomena.

Aesthetic objects are never engaged in vacuo, they are, to put it in Volkenstein’s terms, always judged against a more or less apt ‘thesaurus’. Art is the product of a socio-cultural ‘judgement’ (Nake, 2012, p. 74), artworks have no magical intrinsic qualities, they are objects that display and convey an intentional pattern that generates information. Genres, styles, movements, formal qualities, they are all epistemological constructs deeply entrenched in culture. Art is relational; it arises from the interaction between the object-pattern, the audience, and the context. The value of an artwork depends as much on the way it is in-formed by its creator as on the way it is interpreted and judged by the audience. Without risking exaggeration, this relational process involves a myriad of variables, from perceived technical prowess of the artist to the viewer’s own knowledge and mental state.

It follows that a true measure of aesthetic value should not only account for all the structural elements present in any given artwork and for their mutual interactions, but also for all the potential contexts and thesauruses involved in its interpretation. This of course presumes that somebody has found a way to break down an artwork into objective minimal units and also figured out the rules governing how they are structured and interpreted by a human being. Given the intricacy of both tasks, it is safe to say that attempting to objectively quantify every single one of these variables remains an unfeasible task.

5.3 BEYOND ANALOGUE VS DIGITAL

Granting that artworks are informational systems also shows the ‘analogue vs digital’ dichotomy is an epistemic rather than ontological construction. The difference between analogue and digital is one of encoding; they are both levels of abstraction but with different granularities, they are specifications. Humans experience aesthetic artefacts through the same sensory apparatus despite their purported ontological status; our brains process the information in them just the same. The artwork exists as an object because we impose a level of observation on it, but at the most elemental level what we are always dealing with is information. At a fundamental level, information is indistinguishable and therefore interchangeable, there is no essential difference between one unit and the next one, what we identify as the object-artwork is in truth a stable pattern, the sum and arrangement of a given number of units of information. From this epistemological standpoint there is no necessary ontological distinction between analogue and digital objects. Consequently, this type of informational approach is equally useful for traditional aesthetic artefacts as it is for their digital counterparts.

Volkenstein shows us that the artwork is ‘telling’ us something we did not know, conveying factual information, describing something, a certain view of the world; in so doing something changes, something gets triggered in another system: the viewer’s mind. The work of art as a system is open and in flux. Information begets information, it is something alive, a pattern that is to be constructed. The rarity, the unexpectedness of the potential information generated is what begets value. The artwork is a pretext in the amplest sense of the word; a program with uncertain and unlimited outputs. Birkhoff and the creators of informational aesthetics understood beauty and aesthetic value as something inherent and immutable within the object, while Volkenstein shifts the value to intuition, to the knowledge that falls outside logical proof. For Birkhoff and for informational aesthetics, artistic value is to be discovered and explained, for Volkenstein, it is to be constructed and reimagined. The uniqueness of an artwork is the unquantifiable result of an interaction between minds and of every potential interpretation that can come out of that type of engagement. Volkenstein’s two key points: that (a) artworks may be regarded as complex systems, and (b) artistic value has to do with novelty and irreplaceability but, most of all, with (unlimited) informativeness, represents a valuable contribution to art scholarship. Volkenstein’s model does not enter into contradiction with other interpretations of aesthetic value but complements them; it does not force us to see or to understand artworks just as information, but to see them as different configurations, as types of encoding. Unlimited informativeness is unlimited interpretability, which in turn depends on the individual and its context. Each time we run the artwork-program through an interpreter we obtain a new iteration of a program, which in turn may lead to other programs and variations.

CONCLUSIONS

Regarding artworks as complex systems which, at the very least, ‘say something about something else’ does not alone explain how or what type of information a given artwork might convey; nor does it solve all problems presented by aesthetic experience. What it does show is that any quantitative model attempting to describe aesthetic value is dealing with a complex system whose dynamics cannot be reduced to its individual components. Artworks are not magical objects; regarding them as informational systems places them along other complex human processes. Demystifying art helps us define what it is without the aura of mystery. Art is a very complex (one of the most complex) deliberate forms of communication. Seeing it as information helps to understand it as a communication phenomenon and hence, instead of devaluing or reducing it, it helps explaining it.

What has been offered in this paper is not an outright negation of the possibility of artworks being analysed through quantitative means, but simply an explanation of why it is so difficult to do so. Like all complex problems, recognising the obstacles goes a long way towards finding apt solutions – however modest – and, in the process, learning more about our methodologies. Seeing artworks through an informational perspective can bridge the gap with computational interpretations, which in turn may also work as metaphors that could promote crossfertilisation between programming and art. Finally, we have seen the concept of information is by no means limited to Shannon’s quantitative characterisation, but instead represents a powerful hermeneutical device even in the context of the humanities and the arts. Moreover, it is now clear that an informational characterisation of artworks does not necessarily reduce aesthetic experience to a mindless computational process. Quite the contrary, this type of approach helps to elucidate precisely why art is intrinsically open, mutable and rich.

4. REFERENCES

Adriaans, P., & Van Benthem, J. (2008). Introduction: Information is what information does. In P. Adriaans & J. Van Benthem (Eds.), Philosophy of information (Vol. 8, pp. 7–29). Amsterdam: Elsevier.

Ben-Naim, A. (2007). Entropy demystified: The second law reduced to plain common sense. Singapore: World Scientific.

Ben-Naim, A. (2008). A farewell to entropy: Statistical thermodynamics based on information. Singapore: World Scientific.

Birkhoff, G. D. (1933). Aesthetic measure. Cambridge, Massachusetts: Harvard University Press.

Byfield, T. (2008). Information. In M. Fuller (Ed.), Software studies: A lexicon (pp. 125–132). Cambridge, Massachusetts: The MIT Press.

Cohen, H., Nake, F., Brown, D. C., Brown, P., Galanter, P., McCormack, J., & d’Inverno, M. (2012). Evaluation of creative aesthetics. In J. McCormack & M. d’Inverno (Eds.), Computers and creativity (pp. 95– 111). Berlin; New York: Springer. http://doi.org/10.1007/978-3-642-31727-9_4

Dusek, V. (2006). Philosophy of technology: An introduction. Massachusetts; Oxford: Blackwell Publishing.

Floridi, L. (2004). Information. In L. Floridi (Ed.), The Blackwell guide to the philosophy of computing and information (Vol. 14, pp. 40–61). Oxford: Blackwell Publishing.

Floridi, L. (2010). Information a very short introduction. Oxford; New York: Oxford University Press.

Floridi, L. (2011a). A defence of constructionism: Philosophy as conceptual engineering. Metaphilosophy, 42(3), 282–304. http://doi.org/10.1111/j.1467-9973.2011.01693.x

Floridi, L. (2011b). The philosophy of information. England: Oxford University Press.

Floridi, L. (2016). Semantic conceptions of information. In E. N. Zalta (Ed.), The stanford encyclopedia of philosophy (Spring 2016). Retrieved from http://plato.stanford.edu/archives/spr2016/entries/info rmation-semantic/

Gleick, J. (2011a). Genius: The life and science of Richard Feynman. New York: Open Road Media.

Gleick, J. (2011b). The information: A history, a theory, a flood. New York: Pantheon Books.

Greenberg, C. (1999). Towards a newer Laocoon: An anthology of changing ideas. In C. Harrison & P. Wood (Eds.), Art in theory 1900–1990 (12th reprint, pp. 554–560). Blackwell Publishing.

Klütsch, C. (2012). Information aesthetics and the Stuttgart school. In H. B. Higgins & D. Kahn (Eds.), Mainframe experimentalism: Early computing and the foundations of the digital arts (pp. 65–89). Berkeley: University of California Press.

Mainzer, K. (2004). System: An introduction to systems science. In L. Floridi (Ed.), The Blackwell guide to the philosophy of computing and information (pp. 28–39). Oxford: Blackwell Publishing.

Mignonneau, L., & Sommerer, C. (2006). From the poesy of programming to research as art form. In P. A. Fishwick (Ed.), Aesthetic computing (pp. 169–183). Cambridge, Massachusetts: The MIT Press.

Nake, F. (2012). Construction and intuition: Creativity in early computer art. In J. McCormack & M. d’Inverno (Eds.), Computers and creativity (pp. 61–94). Berlin; New York: Springer. http://doi.org/10.1007/978-3- 642-31727-9_3

Rigau, J., Feixas, M., & Sbert, M. (2008). Informational aesthetics measures. IEEE Computer Graphics and Applications, 28(2), 24–34. http://doi.org/10.1109/MCG.2008.34

Shannon, C. E. (1948). A mathematical theory of communication. The Bell System Technical Journal, 27, 379–423, 623–656. Reprinted with corrections.

Shannon, C. E., & Weaver, W. (1980). The mathematical theory of communication (8th ed.). Chicago: University of Illinois Press.

Taleb, N. N. (2012). Antifragile: Things that gain from disorder. New York: Random House.

Volkenstein, M. V. (2009). Entropy and information. (A. B. de Monvel & G. Kaiser, Eds., A. Shenitzer & R. G. Burns, Trans.). Berlin: Birkhäuser.

Weaver, W. (1949). The mathematics of communication. Scientific American, 181(1), 11–15.

Wiener, N. (1985). Cybernetics: Or control and communication in the animal and the machine (2d ed.). Cambridge, Massachusetts: The MIT Press.

BIOGRAPHICAL INFORMATION

Rodrigo Hernández-Ramírez (Mexico City, 1982) is a PhD candidate (ABD) in the Faculty of Fine Arts at the University of Lisbon, Portugal. He is a member of the Centre for Research and Studies in Fine Arts (CIEBA) at the same institution. His research interests include new media, philosophy of technology, and photography. His current research focuses on the ontology of computational aesthetic objects as seen through the lens of philosophy of information and postphenomenology.

Rodrigo Hernández-Ramírez
Faculty of Fine Arts,
University of Lisbon,
Portugal

rodrigo.hr@protonmail.ch

NOTES

CITAR Journal, Volume 8, No. 1 – Special Issue: xCoAx 2016